Matemáticas (plan 1983) 2022-2

Optativas de los Niveles V y VI, Sistemas Dinámicos Discretos I

Modalidad Híbrida: Presencial con transmisión por Zoom

• Ya se han realizado pruebas y al parecer la red funciona bien (pues no hay mucha gente en la facultad y no se satura).
• Se usará un pizarrón virtual (OpenBoard), de modo que en el salón de clases con proyección y en la transmisión por Zoom verán exactamente lo mismo.

Importante

Vínculo al Zoom del curso:

https://cuaieed-unam.zoom.us/j/83289007714

La presentación del curso se realizarán los días Lunes 14, Miércoles 16 y Viernes 18 de Febrero a las 10 am, por Zoom. El inicio del curso será el Lunes 21 de Febrero.

Las clases se realizarán:

• En línea por Zoom hasta el 12 de Marzo.
• De manera presencial con transmisión en vivo por Zoom desde el salón después del 12 de Marzo.
• Por el profesor Lunes, Miércoles y Viernes en el horario asignado.
• Por la ayudante Martes y Jueves en el horario asignado.

Temario

En este curso se introduce al estudio de los sistemas dinámicos discretos en 1 dimensión real (es decir, en subconjuntos de ℝ o el círculo) y en espacios métricos generales (área llamada dinámica topológica). El curso estará dividido en 4 unidades:

1. Conceptos básicos de dinámica topológica y dinámica en ℝ. (Unidad Febrero-Marzo.)

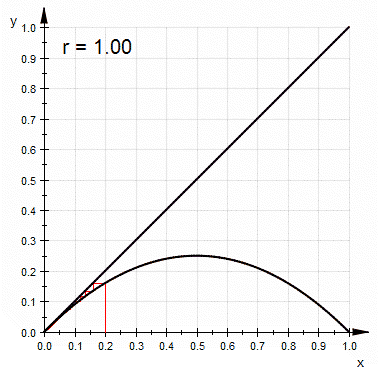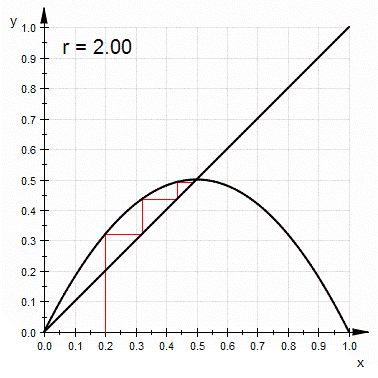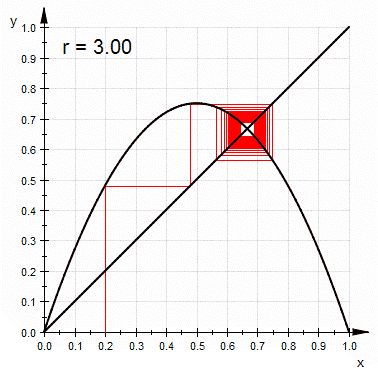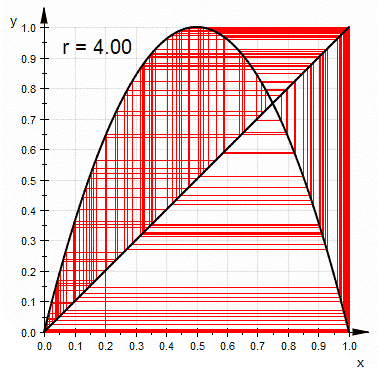
a) Introducción.

Modelos de poblaciones. Métodos numéricos iterativos. Sistemas Dinámicos y Sistemas Dinámicos Discretos.

b) Conceptos básicos.

Iteradas e Iteraciones. Órbitas. Puntos Fijos, Periódicos y Pre-Periódicos.

c) Hiperbolicidad.

Puntos Atractores y Repulsores. Puntos Neutros. Teoremas de Hiperbolicidad.

d) Herramientas Visuales.

Retrato Fase. Análisis Gráfico.

e) Teorema de Sharkovsky.

Teorema de Li-Yorke. Teorema y Orden de Sharkovsky. La duplicadora.

2. Caos y Estabilidad. (Unidad Marzo-Abril.)

a) Estabilidad.

Órbitas asintóticamente periódicas. El ω-conjunto límite. Estabilidad de Lyapunov.

b) Caos.

Sensibilidad a las condiciones iniciales. Transitividad Topológica. Órbitas Densas. Teorema de Jacobi. Definición de Caos de Devaney.

c) Conjugación Topológica.

Propiedades dinámicas que se conservan bajo conjugación. Equivalencia de sistemas.

d) Medidas de Estabilidad y Caos.

Exponentes de Lyapunov. Entropía Topológica.

3. Dinámica Simbólica. Dinámica de Homeomorfismos en el Círculo. (Unidad Abril-Mayo.)

a) Dinámica Simbólica.

La función corrimiento en el espacio sucesiones de N símbolos. Itinerarios. El Conjunto de Cantor. Subcorrimientos de tipo finito. La sumadora de Misiurewicz.

b) Homeomorfismos en el Círculo.

Homeomorfismos y Levantamientos. El Número de Rotación.

4. Bifurcaciones y Estabilidad Estructural. (Unidad Mayo-Junio.)

a) Familias de Funciones.

Diagramas de Órbitas. Diagramas de Bifurcación.

b) Bifurcaciones.

Bifurcación Tangente. Bifurcación de Duplicación del Periodo. Teoremas de existencia de bifurcaciones. Otras bifurcaciones.

c) Familia Logística.

Análisis de Bifurcaciones. Zona Caótica. Ventanas del Diagrama. Ejemplo de Renormalización.

d) Estabilidad Estructural.

Espacios de funciones. Ejemplos de Estabilidad Estructural. El Lema de Cierre en el Círculo.

Pre-requisitos

Opcional: Topología I.

Evaluación

Modo híbrido (presencial y con alumnos en línea ó presencial sin ayudante)

• 80%. Cuatro tareas-examen, una por unidad.
• 20%. Un proyecto de investigación.

(En el caso que sólo haya alumnos presenciales...

Modo presencial (con ayudante)

• 40%. Cuatro tareas, una por unidad.
• 50%. Cuatro exámenes, uno por unidad. Se permiten reposiciones de todos los exámenes, máximo 2 reposiciones.
• 10%. Una exposición con duración de 30 minutos, a realizarse a finales del mes de Junio. Ó el desarrollo de una pequeña investigación
• Para derecho a exámenes de reposición y examen final, haber presentado al menos 2 exámenes y haber entregado al menos 2 tareas.

)

Temas propuestos para exposición o investigación: Teoremas sobre la definición de Caos de Devaney, Resultados de Entropía Topológica, El Atractor de Sistemas de Funciones Iteradas, La Constante de Feigenbaum, La Derivada Schwarziana, Dinámica en Hiperespacios, Las Lenguas de Arnol'd, Secuencias Sturmianas, y muchos otros.

Bibliografía

• Principal.
  • King, Jefferson E. & Méndez, Héctor. Sistemas Dinámicos Discretos. 2014.
  • Devaney, Robert L. An Introduction to Chaotic Dynamical Systems. 1989.
• Complementaria.
  • Robinson, R. Clark. Dynamical Systems: Stability, Symbolic Dynamics, and Chaos. 1995.
  • Brin, Michael & Stuck, Garrett. Introduction to Dynamical Systems. 2004
  • Devaney, Robert L. A First Course in Chaotic Dynamical Systems-Theory & Experiments. 1992.
  • Alligood, K., Sauer, T.D. & Yorke, J. CHAOS, an Introduction to Dynamical Systems. 1996.